AN INTRODUCTION

The algorithm I'll be using to generate a voronoi diagram will be the Fortune Sweep algorithm. This maintains both a sweep line and a beach line, which both move through the plane as the algorithm progresses. The sweep line is a straight horizontal line moving from top to bottom down the plane. At any time during the algorithm, the input points above the sweep line will have been incorporated into the voronoi diagram, while the points below the sweep line will not have been considered yet.

The beach line is not a straight line, but a complicated, piecewise curve above the sweep line, composed of pieces of parabolas; it divides the portion of the plane within which the Voronoi diagram can be known, regardless of what other points might be below of the sweep line, from the rest of the plane.

For each point above the sweep line, one can define a parabola of points equidistant from that point and from the sweep line; the beach line is the boundary of the union of these parabolas. As the sweep line progresses, the vertices of the beach line, at which two parabolas cross, trace out the edges of the Voronoi diagram. The beach line progresses by keeping each parabola base exactly half way between the points initially swept over with the sweep line, and the new position of the sweep line. Mathematically, this means each parabola is formed by using the sweep line as the directrix and the input point as the focus.

My version of the algorithm maintains a linked list describing the combinatorial structure of the beach line, and a priority queue listing potential future events that could change the beach line structure. There are two types of events:

Site
Circle

The site event is the addition of another parabola to the beach line (when the sweep line crosses another input point). The circle event is the removal of a curve from the beach line (when the sweep line becomes tangent to a circle through some three input points whose parabolas form consecutive segments of the beach line). Each such event may be prioritised by the y-coordinate of the sweep line at the point the event occurs. The algorithm itself then consists of repeatedly removing the next event from the priority queue, finding the changes the event causes in the beach line, and updating the data structures.

[ Site Events ]

Find the occurrence of a region in the beach line, containing the input point
Create new boundary rays with the input point
Rebuild the beach line
Remove circle events not needed
Check to see if we need to add another two circle events

[ Circle Events ]

Calculate the intersection of the two edges, either side of the current node
Create a new boundary ray between the left neighbour of the left edge, and the right neighbour of the right edge
Replace the two edges and the current node with the new boundary ray
Output the two edges to an edges array
Remove any circle events now not needed
Check to see if we need to create new circle events

[ Cleanup Operations ]

Finish any remaining edges in the beach line, checking for intersection with the boundary

Event Methods

[ Site Event - Add to the beach line ]

We add to the beach line when the sweep line hits a new point. For this we need to find out within the beach line which parabola the input point is under.

See find the occurrence of the region in the beach line containing the input point

We store a reference to the parabola we found in the step above. Next, we create two edges. One either side of the new node we’re inserting. Whilst we create two edges they appear as one, each sharing the same starting point but pointing in opposite directions.

See create new edges with a site event

With the two new edges we can rebuild the beach line. We first duplicate the parabola node we found in the first step. We then take the two edges and rebuild the beach line as per the diagram below.

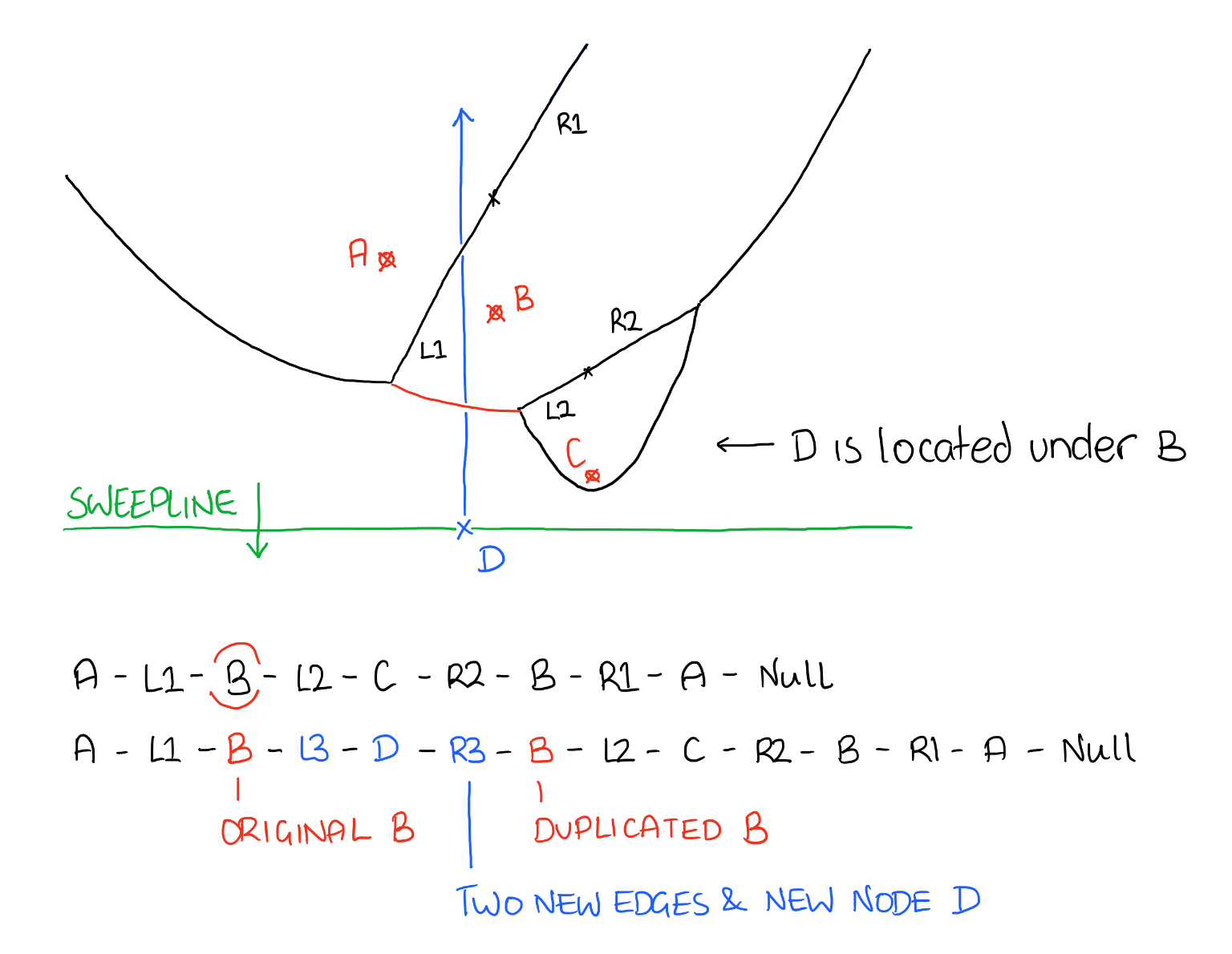
As we can see in the diagram above we have now changed the structure of the beach line, we have inserted a couple of new edges. Because of this we need to remove any circle events from the parabolas/nodes either side of the parabola found in step one. We also need to remove these from the event queue.

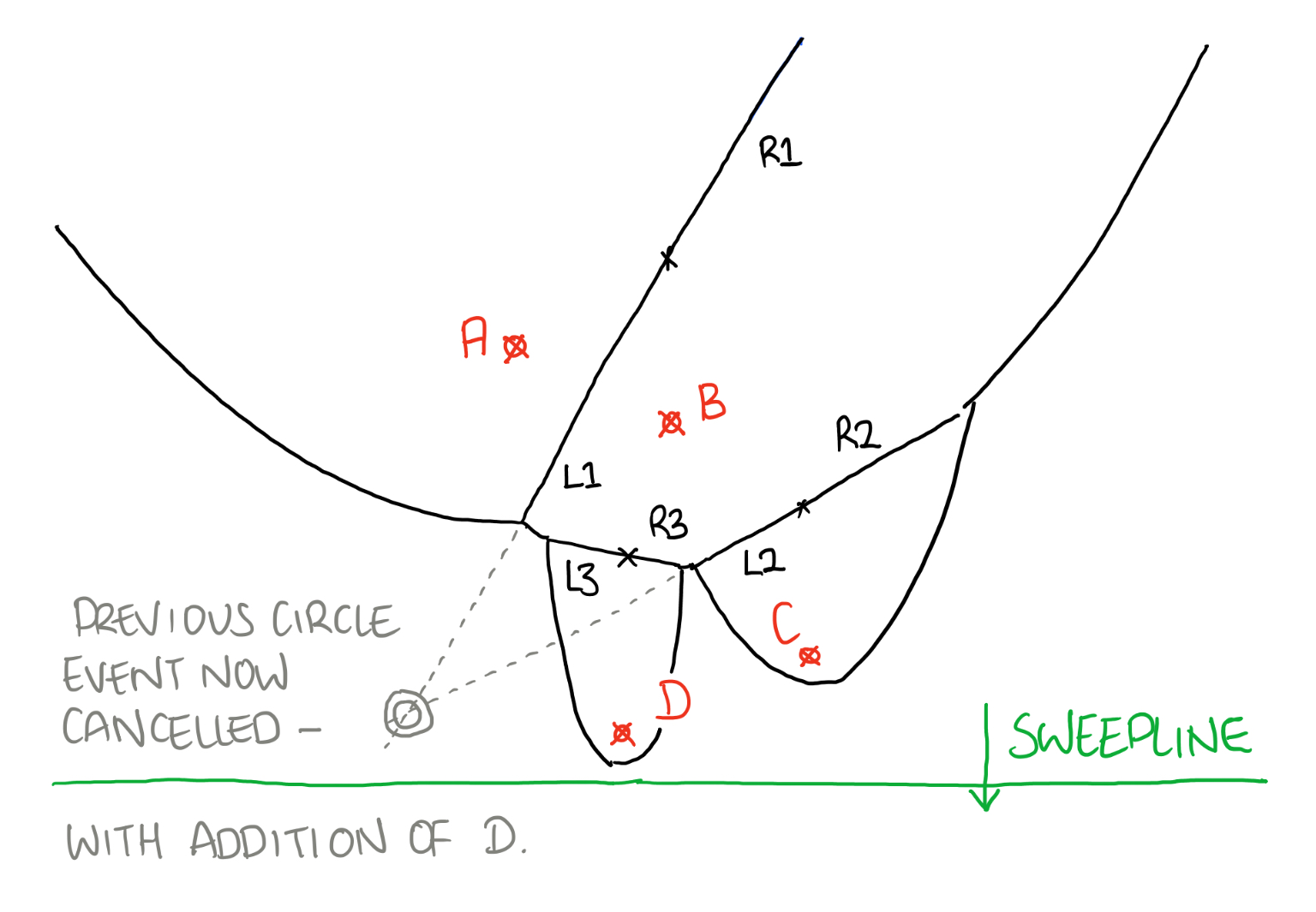
See remove circle events not needed

Finally we need to check for two new circle events, we only need to check what has changed, in this case we need to check the original parabola, and also the copy that was made of this parabola.

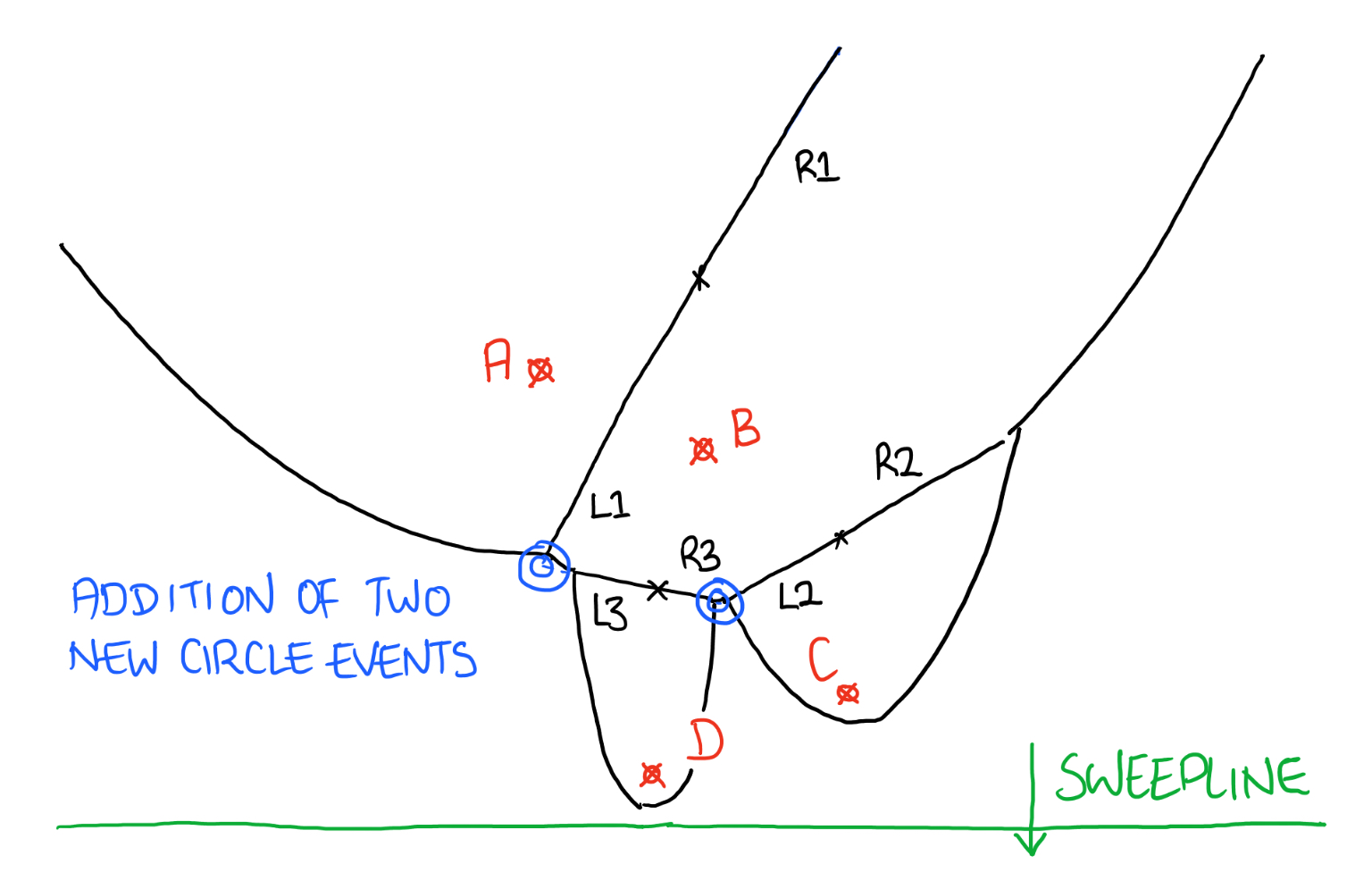
See check to see if a circle event is needed

[ Circle Event - Remove from the beach line ]

Only occurs during a circle event, when we need to remove two edges and a parabola from the beach line. First things first we take the parabola node, and it’s adjacent neighbours (the edges) and close these off at the intersection point. This is as simple as finding the intersection point and assigning their end point to this intersection point.

See calculate the intersection between two edges

With both of these edges gaining an end point we can add these to the final edges array which will be drawn to the screen. Next we construct a new edge from the neighbours edges, the left neighbour of the left edge and the right neighbour of the right edge.

See create a new edge from a circle event

Once this is done we simply remove the parabola node and it’s adjacent edges from the beach line and insert the new edge in their place.

Other Methods

[ Create New Edges With a Site Event ]

First we need to calculate a starting point for these two edges, they share the same starting point and point in opposite directions.

Each edge object contains four parameters:

Start, a 2D coordinate denoting the start point of the edge
Direction, a 2D vector denoting the direction of the edge
M, the gradient
C, the crossing point with y axis where x = 0

For the starting point of these edges we know the x coordinate, it’s just the x coordinate of the input point. We just need to calculate the y coordinate, this is where a ray pointing vertically upwards intersects with the parabola.

See find y coordinate of input point where it intersects with a parabola above it.

Next we calculate the Direction. This is done as follows.


        Direction = ( -1 * (left.y - right.y), left.x - right.x )

Then we calculate the gradient, m. If we draw a line between the generating points the edge would be perpendicular to this line, every point on this edge is equidistant between the left point and the right point.


        M = -1 / ((left.y - right.y) / (left.x - right.x))

Finally we can calculate the crossing point with the y axis, C. We use the equation of a line here (y = mx + c) and place in the values for the gradient, and the starting x and y coordinate to get C.


        C = start.y - M * start.x

[ Remove Circle Events Not Needed ]

This is just a case of checking to see if the node passed into the function has a circle event associated with it. If it does we remove it, by setting it to null and we also then check through the event queue and remove it from there.

For this we just pass through each element in the queue, if it matches with the one we’re testing we remove it from the queue and stop searching.

[ FIND Y COORDINATE OF INPUT POINT WHERE IT INTERSECTS WITH A PARABOLA ABOVE IT ]

We know the equation of a parabola:


        y = ax^2 + bx + c

Where:


        a = 1 / 4p

        b = -h / 2p

        c = (h^2 / 4p) + k

        x = x coordinate of input point

And:


        p = the distance between the parabolas focus and its vertex OR

            distance from the parabolas vertex to its directrix (the sweep line), therefore

        p = ( focus.y - sweepline.y ) / 2

        

        h, k = x, y of parabolas vertex, therefore

        h = focus.x

        k = focus.y  - p

To get y simply input the x value of the input point into the equation above.

[ FIND THE OCCURRENCE OF THE REGION IN THE BEACH LINE CONTAINING THE INPUT POINT ]

The beach line is stored as a reference to the first node in the linked list. The general structure of the beach line is a parabola, edge, parabola, edge, then parabola, and so on and so on.

I search through each pair of parabolas and edges and work out where the edge intersects the parabola.

See parabola edge intersection.

If the x value of the new point is less than the parabola/edge intersection x value then we know that the new point is under this parabola. If it isn’t we just keep testing each pair of parabola and edges until we find a match.

[ PARABOLA EDGE INTERSECTION ]

First I need to get the equation of the current parabola with respect to the current sweepline.y value.

See get the equation of a parabola

We know the edges gradient at point it crosses the x = 0 axis, these are stored as variables in the edges properties as m and c respectively. We can set the y coordinate for the line equal to the y coordinate for the parabola. Remember that the edge equation and the parabola equations are as follows:


        For the edge; y = mx + c where m is gradient, c is y intercept

        For the parabola; y = ax^2 + bx + c

Subtract one from the other to give y:


        y = ax^2 + (b - m)x + (c - c)

In summary:


        y = ax^2 + bx + c

Where:


        a = parabola.a

        b = parabola.b - edge.m

        c = parabola.c - edge.c

We can plug these values into the quadratic formula:


        discriminant = b*b - 4ac

        x1 = ( -b + sqrt( discriminant )) / 2a

        x2 = ( -b - sqrt( discriminant )) / 2a

This gives us two locations where the line crosses the parabola. Remember we’re not dealing with lines, but technically with rays, they have a starting point and a direction. In that case we only want one of these x values. The one I select depends on the direction of the edge, if it’s pointing right we select the highest value, if it’s pointing left we select the minimum value:


        min = x1 < x2 ? x1 : x2

        max = x1 > x2 ? x1 : x2

        x = edge.direction.x < 0 ? min : max

[ GET THE EQUATION OF A PARABOLA ]

Finds the equation of the parabola in a similar way to the method described in find y coordinate of input point where it intersects with a parabola above it.

That is:


        k = ( focus.y + sweepline.y ) / 2

        p = ( focus.y - sweepline.y ) / 2

        a = 1 / 4p

        b = ( -1 * focus.x ) / 2p

        c = ( focus.x^2 / 4p ) + k

Where a, b and c represent the equation of the parabola in the form:


        y = ax^2 + bx + c

[ CHECK TO SEE IF CIRCLE EVENT IS NEEDED ]

First we need to get references to both the left and right edges for the current node (parabola). With these we find out if these edges intersect with each other.

See calculate the intersection between two edges

We now now know if the two edges will intersect at some point in the future. If they will we need to add a circle event to the event queue. For this we need to add a trigger point, this will be triggered when the sweep line hits the bottom of the circle.

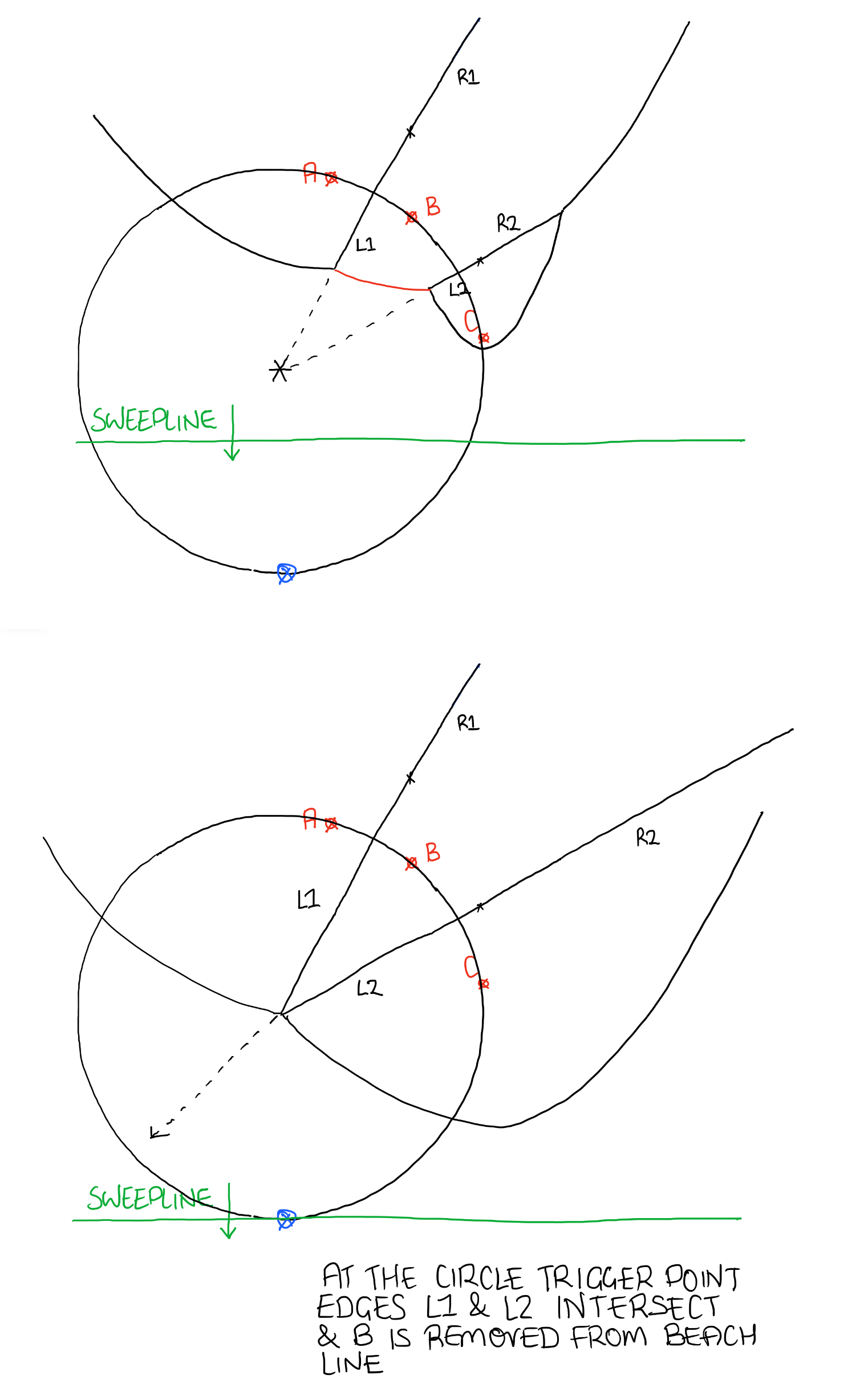
We know the coordinate of the potential intersection point, and the coordinate of the current node. With this we can work out the radius of the circle and use this to find out the potential trigger point:


        dy = focus.y - intersection.y

        dx = focus.x - intersection.x

        radius = sqrt( dy^2 + dx^2 )

Notice I said ‘potential’ trigger point, this is because the trigger point may have already been passed by the sweepline. If this is the case we simply ignore it. If the trigger point hasn’t been passed only then can we create a circle event with the trigger point.


        If (intersection.y - radius > sweepline.y) Then return Null

        Else create new circle event with (intersection.x, intersection.y - radius)

[ CALCULATE THE INTERSECTION BETWEEN TWO EDGES ]

We can find the intersection between two lines quite easily, firstly we just check to make sure they are not parallel. We can do this by ensuring the gradient for each edge are not equal to each other.


        If (leftedge.m == rightedge.m) Then return Null

Next we just set the two edges equal to each other to find x:


        leftedge.m * x + leftedge.c = rightedge.m * x + rightedge.c

        (leftedge.m + rightedge.m)x + leftedge.c = rightedge.c

        (leftedge.m + rightedge.m)x = rightedge.c - leftedge.c

        x = (rightedge.c - leftedge.c) / (leftedge.m + rightedge.m)

We now have the x value, we can calculate the y value by substituting the x value into one of the line equations:


        y = leftedge.m * x + leftedge.c

We now have a potential crossing point (x , y). Bear in mind we’re not dealing with lines, we’re dealing with rays, they have a start point and a direction. We need to make sure the intersection point is not on the other side of the ray.

We can check this with the following tests. I check the direction between the edges start point and the potential intersection point and compare this with the edges direction vector. If they are different polarities then the edge is not going in the correct direction and therefore there is no intersection:


        If ((x - leftedge.start.x) / leftedge.direction.x < 0) Then return Null

        If ((y - leftedge.start.y) / leftedge.direction.y < 0) Then return Null

        If ((x - rightedge.start.x) / rightedge.direction.x < 0) Then return Null

        If ((y - rightedge.start.y) / rightedge.direction.y < 0) Then return Null

If all these tests pass we have an edge - edge intersection at point (x, y).

[ CREATE A NEW EDGE FROM A CIRCLE EVENT ]

We know the starting point of this new edge, we calculated this when we worked out the end points of the two edges which triggered this circle event.

Next we calculate the direction, gradient and y intercept. For this we need the left and right sites, this is simple we just traverse through the beach line. We can now calculate the direction. This is done as follows:


        d = ( -1 * (left.y - right.y), left.x - right.x )


        m = -1 / ((left.y - right.y) / (left.x - right.x))

Finally we can calculate the crossing point with the y axis, c. We use the equation of a line here (y = mx + c) and place in the values for the gradient, and the starting x and y coordinate to get c.


        c = start.y - m * start.x