AN INTRODUCTION  

My initial interest in virtual reality comes from the fact I used to spend a lot of my time producing 3D models, combined with the fact it's quite easy to produce a virtual reality app using something like Google Cardboard. What does become more of an issue is ensuring your images are in the correct format, some packages will require an equirectangular image which is based on a sphere. And some will require a simple cube map - which is obviously based on a cube! We could really do with a program or script which converts between the two formats.

What is an equirectangular image?

An equirectangular image is a simple way of representing a spherical object as a flat 2D image. The projection maps meridians to vertical straight lines of constant spacing, and circles of latitude to horizontal straight lines of constant spacing. Common examples include most world maps, an example of this type of projection is shown below:

What is a cube map?

A cube map is pretty much what it sounds like - its a collection of six images representing the six faces of a cube. The environment is projected onto these cube faces in a similar way to the equirectangular image, the only difference being that we're using a cube instead of a sphere. They are traditionally used a lot in producing sky boxes for games. An example of this using the image above as an input is shown below:

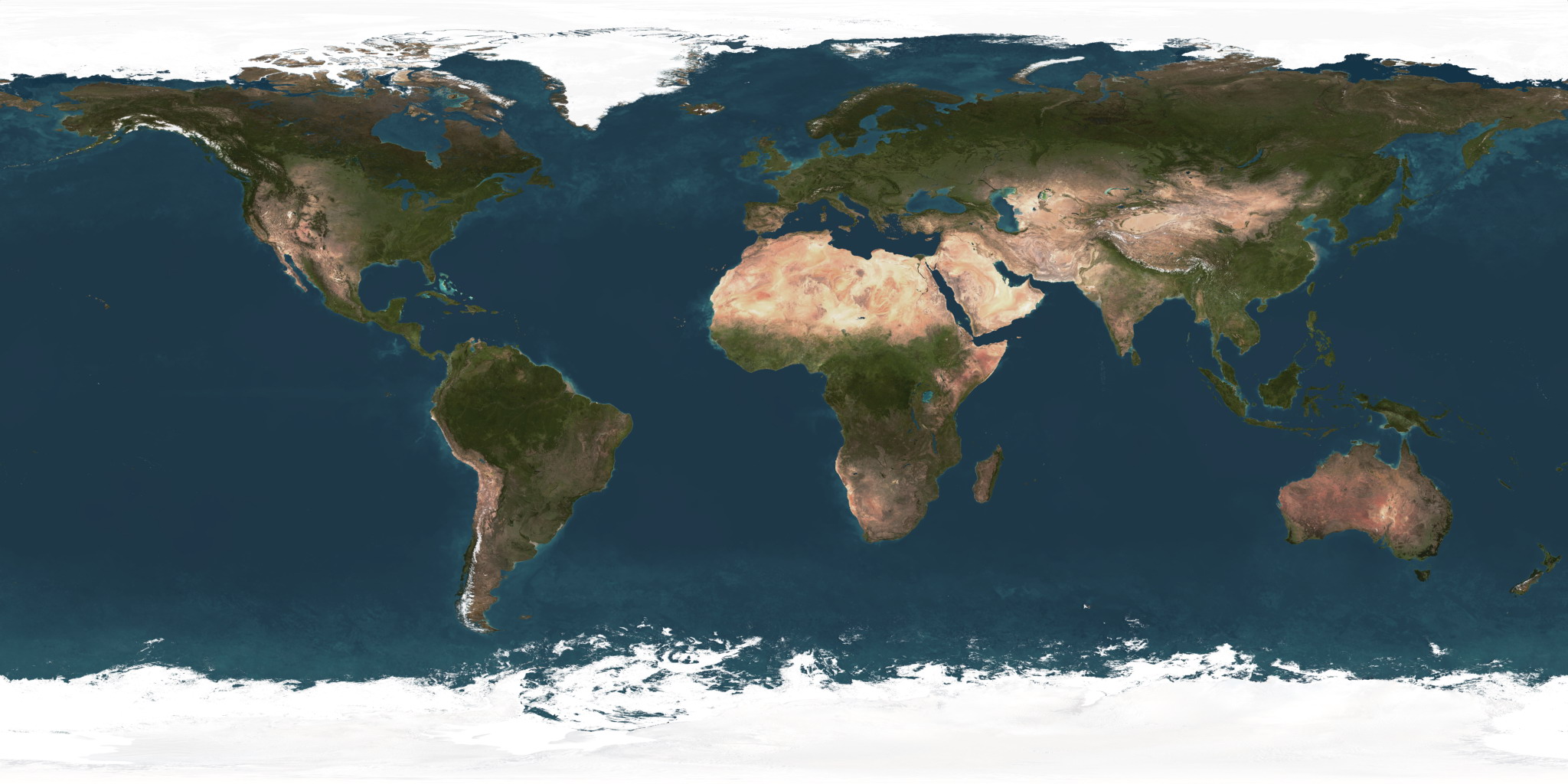
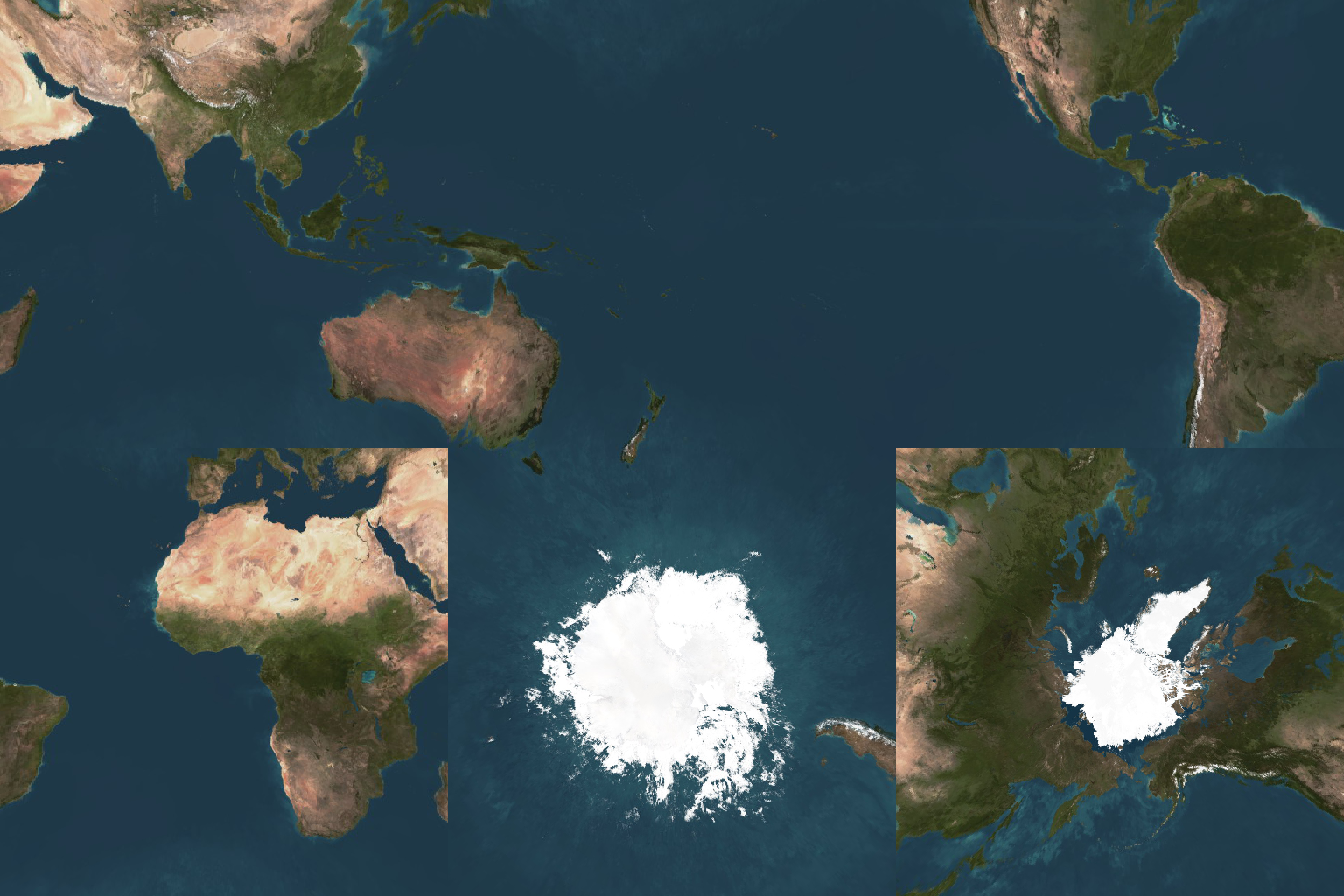
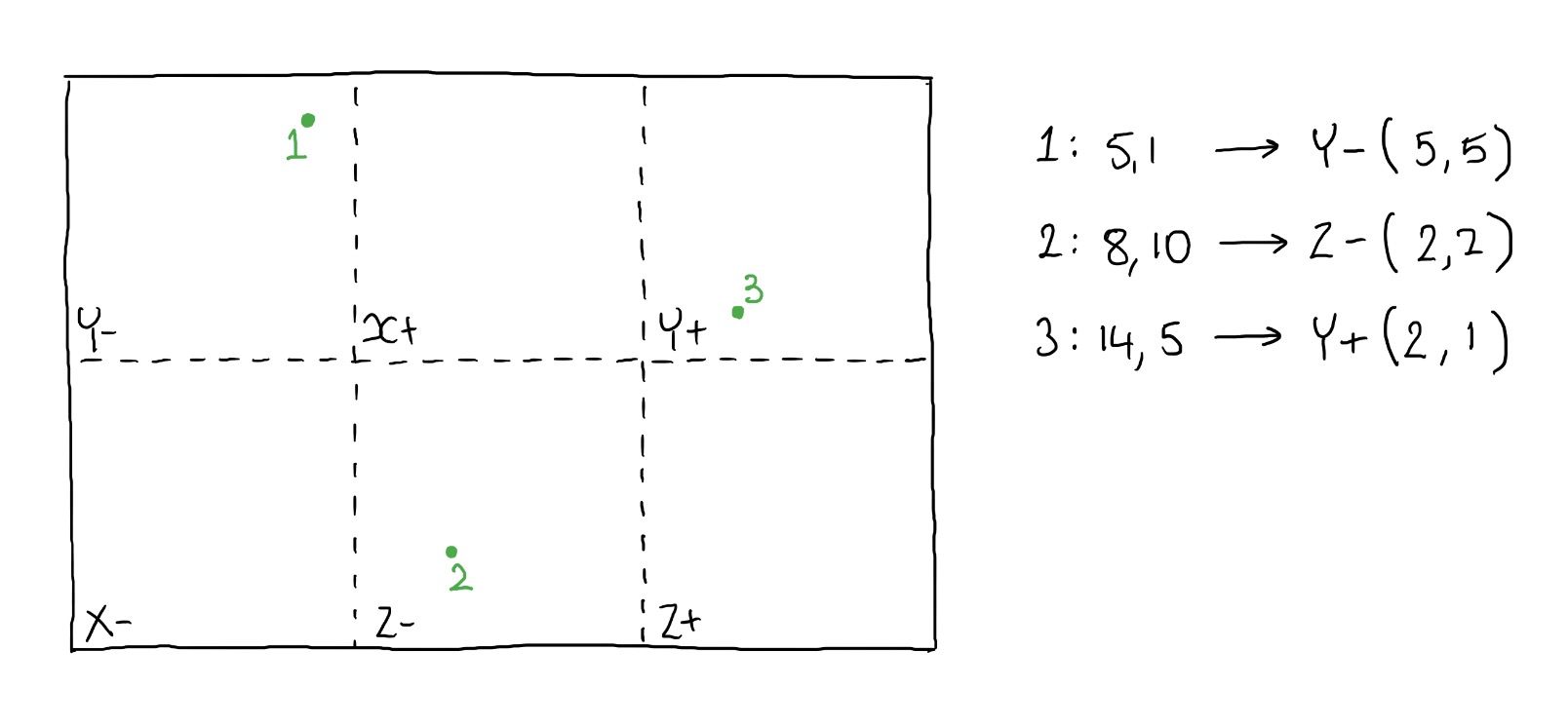
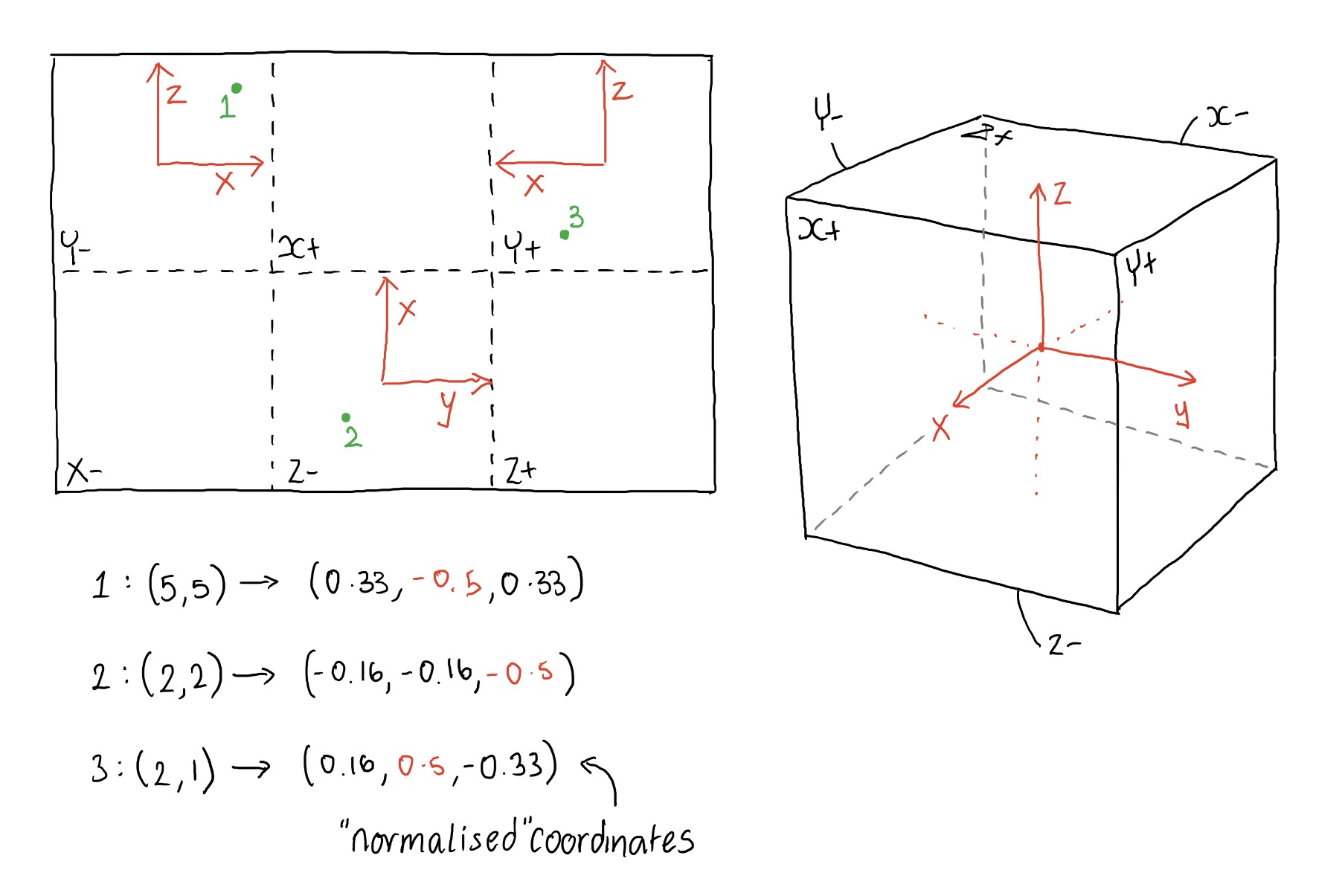
SPHERICAL COORDINATES

Firstly we need to calculate the spherical coordinates for each pixel in the output equirectangular image. If the coordinates in the equirectangular image are x and y; and the width & height of this image are w, h respectively then the normalised coordinates (u, v) ranging from 0 - 1 are given by:

u = x / w
v = y / h

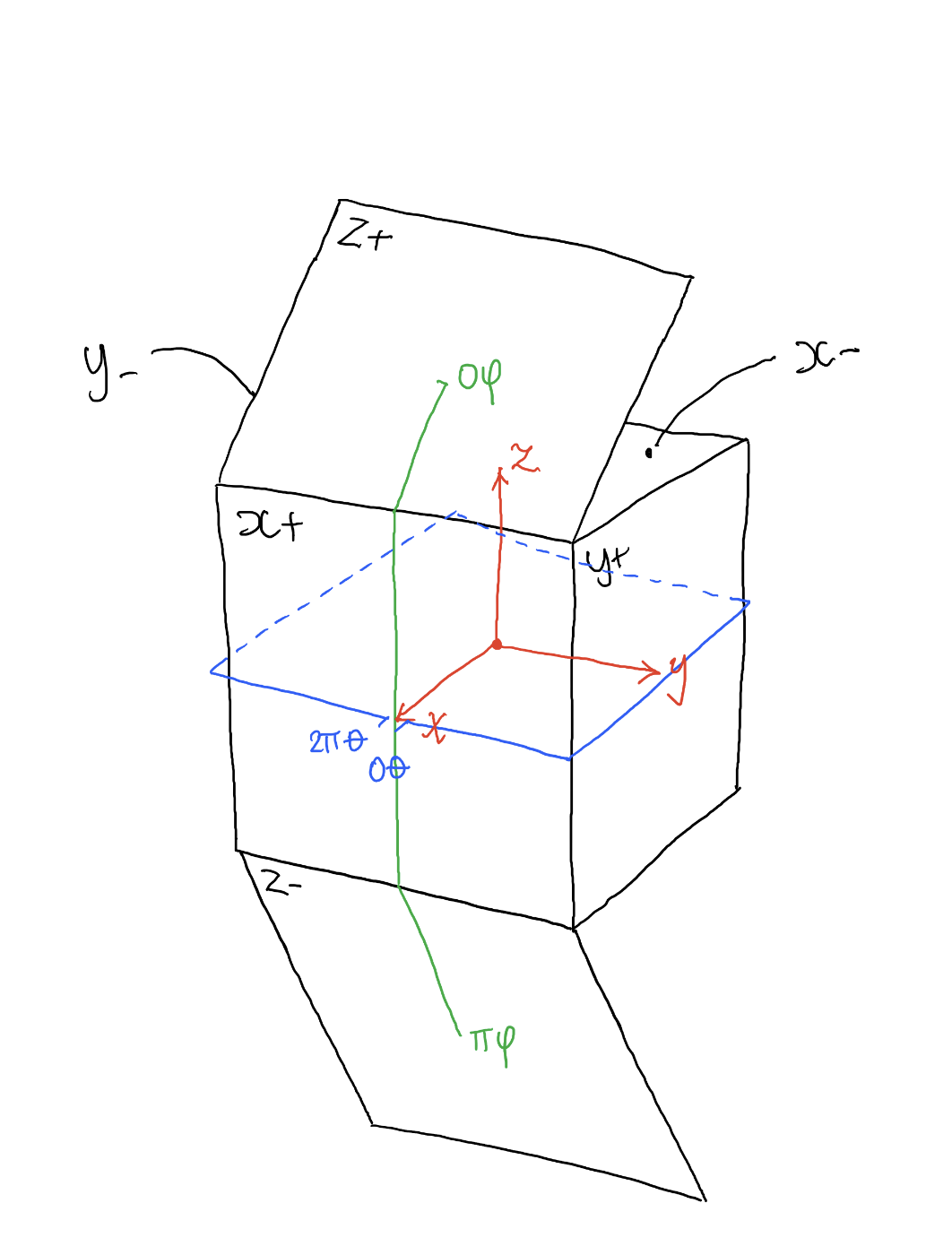
The spherical coordinates θ and φ are calculated from the normalised coordinates u, v. θ is defined to be the angle in the xy plane from the X+ axis with 0 ≤ θ ≤ 2π. φ is defined to be the polar angle from the positive Z axis with 0 ≤ φ ≤ π:

θ = u*2π
φ = v*π

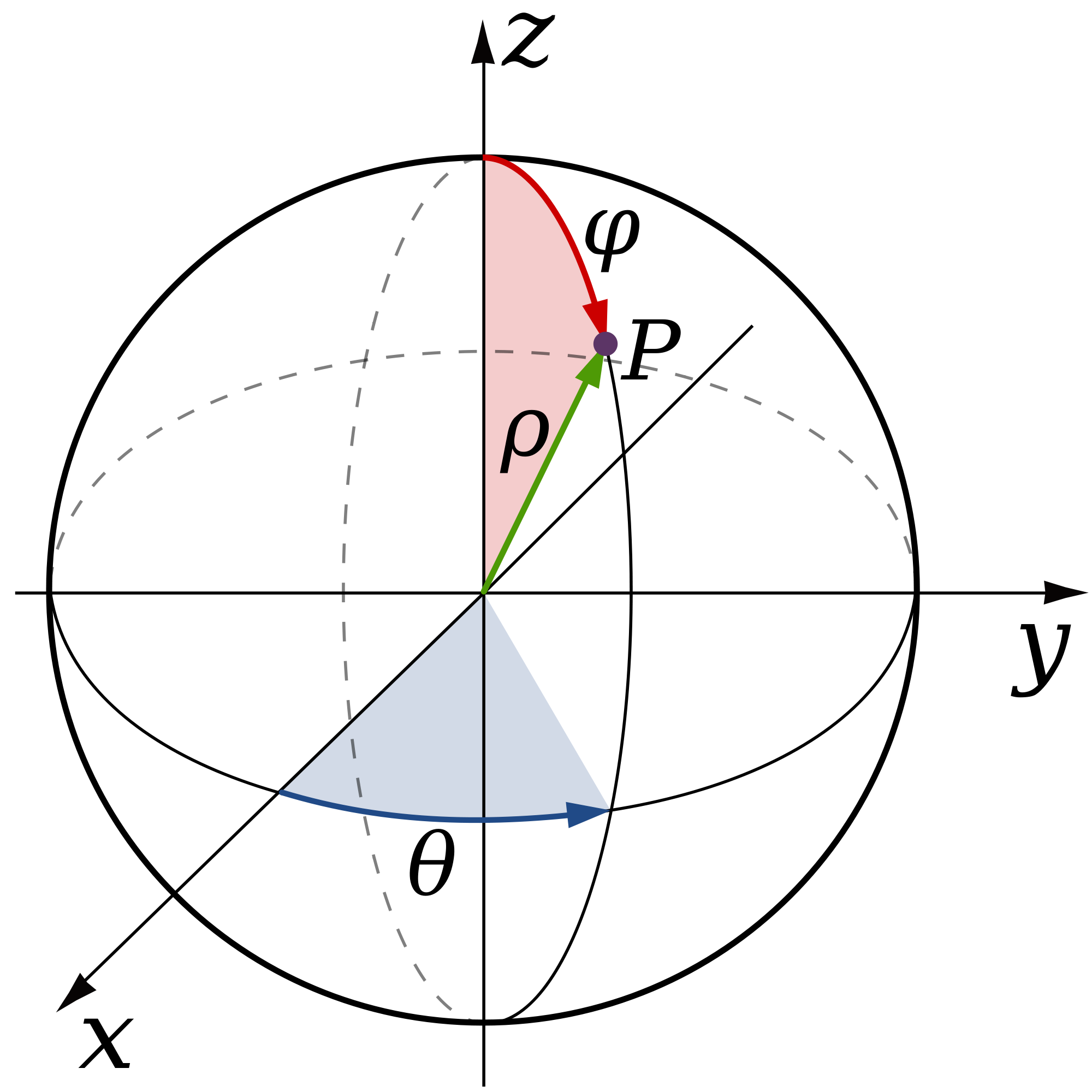
CARTESIAN COORDINATES

Now we can use the 3D polar coordinates to form a unit vector and work out which face of the cube we're pointing towards. We can do this by using the following equations, note that 'r' has been removed as we're producing a unit vector (the distance in this this is one therefore there's no need to include this):

x = cosθsinφ
y = sinθsinφ
z = cosφ

Next we find the maximum absolute value; then divide each of these coordinates by this value. This means either xx, yy or zz will equal positive or negative one. Whichever of these does is the largest value, and the sign will indicate whether it's positive or negative. So, for example if 'xx' equals +1 then it means that the ray is mainly pointing towards the positive x face:

maximum = max(abs(X),abs(Y),abs(Z))
xx = x / maximum
yy = y / maximum
zz = z / maximum

As demonstrated in the image below:

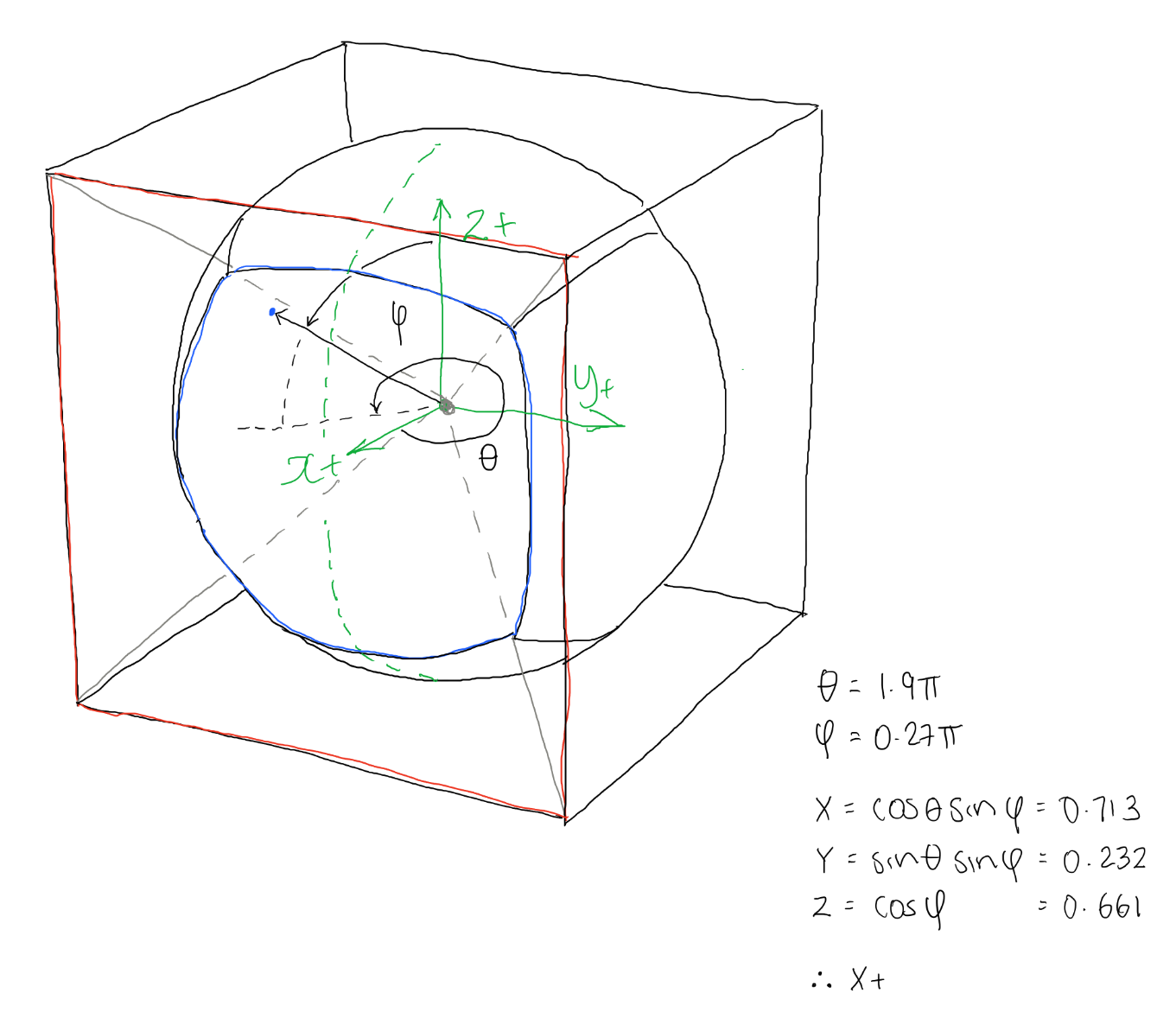
So for example in the image above we can we can see that xx = 0.713, yy = -0.232 and zz = 0.661. The maximum absolute value of this is 0.713, for x. And it's positive so we know the face this ray is mainly pointing towards is the X+ face.

3D PROJECTION

By this point we know which direction the ray is pointing in and which cube face it will hit. Knowing this information allows us to calculate the distance from the centre of the sphere to the point where it intersects with the cube map.

if(xx==1 or xx==-1):
    projectX(theta,phi,xx)
else if (yy==1 or yy==-1):
    projectY(theta,phi,yy)
else:
    projectZ(theta,phi,zz)

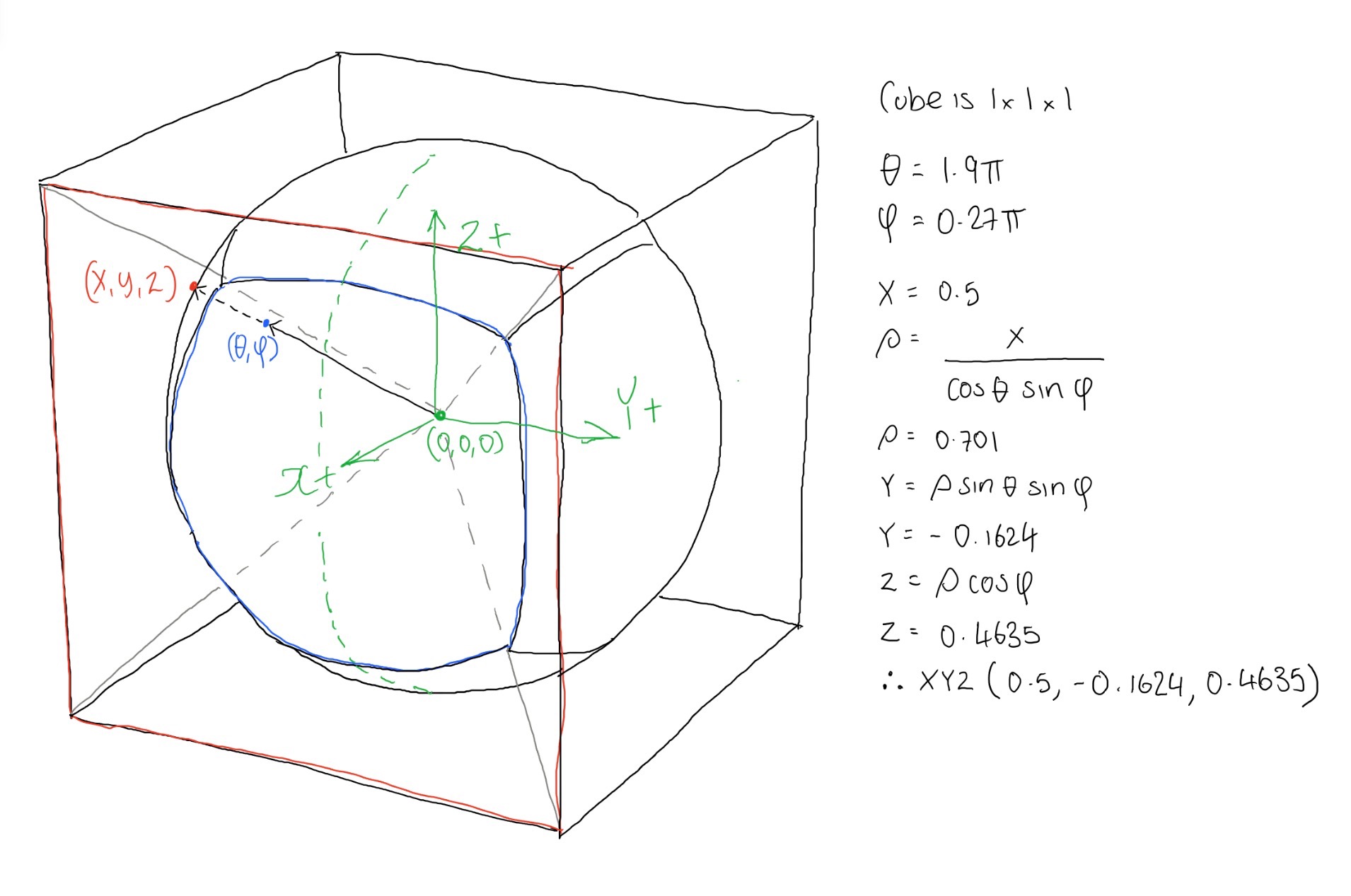
So we now know which face we're pointing towards. We can use this information to help work out the coordinates for where the ray hits the cube face. If for example we're selecting the X+ face we know the coordinate where the ray intersects the cube will at least have an X coordinate that matches half the length of one of the cube map lengths. In my code I just assume a cube of size 1x1x1 centred on (0,0,0). Therefore the X coordinate in this case will be 0.5:

def projectX(theta,phi,sign):

    x = sign*0.5
    rho = x/(cos(theta)*sin(phi))
    y = rho*sin(theta)*sin(phi)
    z = rho*cos(phi)
    return (x,y,z)

As you can see demonstrated below:

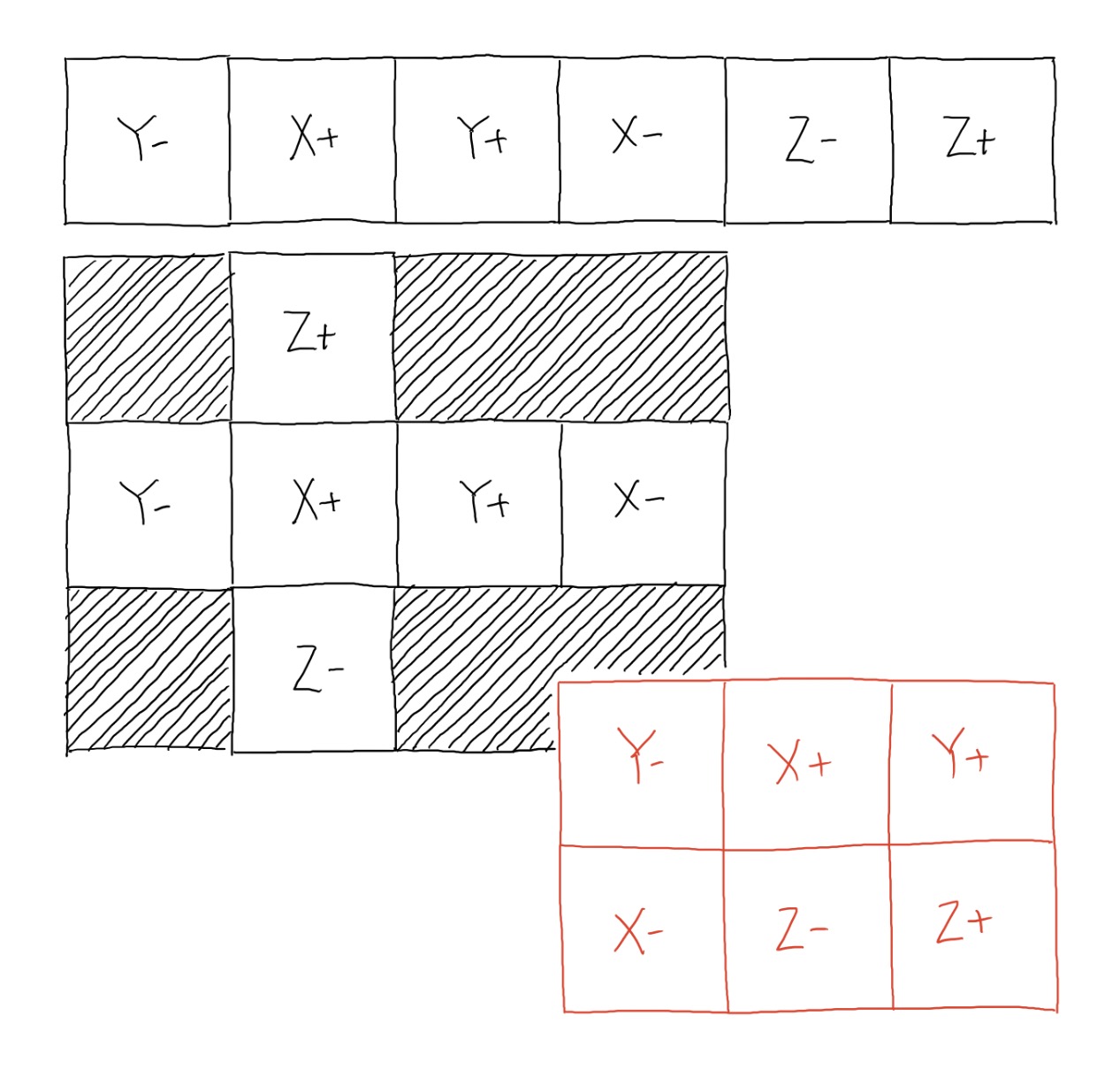
2D CUBEMAP PIXEL

Now we have the coordinate of where we need to extract a colour from the cube map. Currently this coordinate is 3D and is located somewhere on a cube which has dimensions 1 x 1 x 1. Now, we know that the cube is broken down into the following faces (shown slightly unfolded):

We know it's broken down like this for a number of reasons:

1. We know θ is in the XY plane, from the positive X axis and has a total range of 2π radians. This means the X+ face is split in two, less than 0.25π & greater than 1.75*π
2. We know that for equirectangular images as we increase θ we travel from X+, Y+, X- and so on, anti-clockwise.
3. When φ = 0 we're pointing towards the top of the cube, therefore at the Z+ face, when φ is π it is pointing directly downwards at the Z- face.

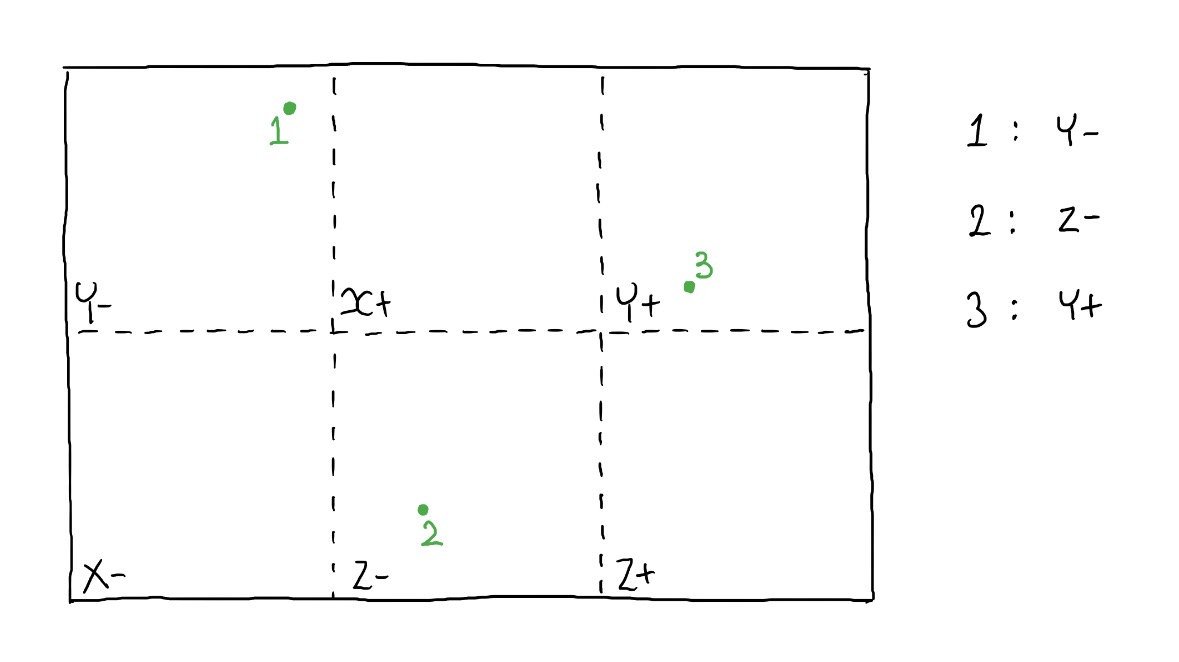
We need to convert the 3D coordinates to a 2D coordinate. As you can see in the images above and below you can see this isn't a simple case:

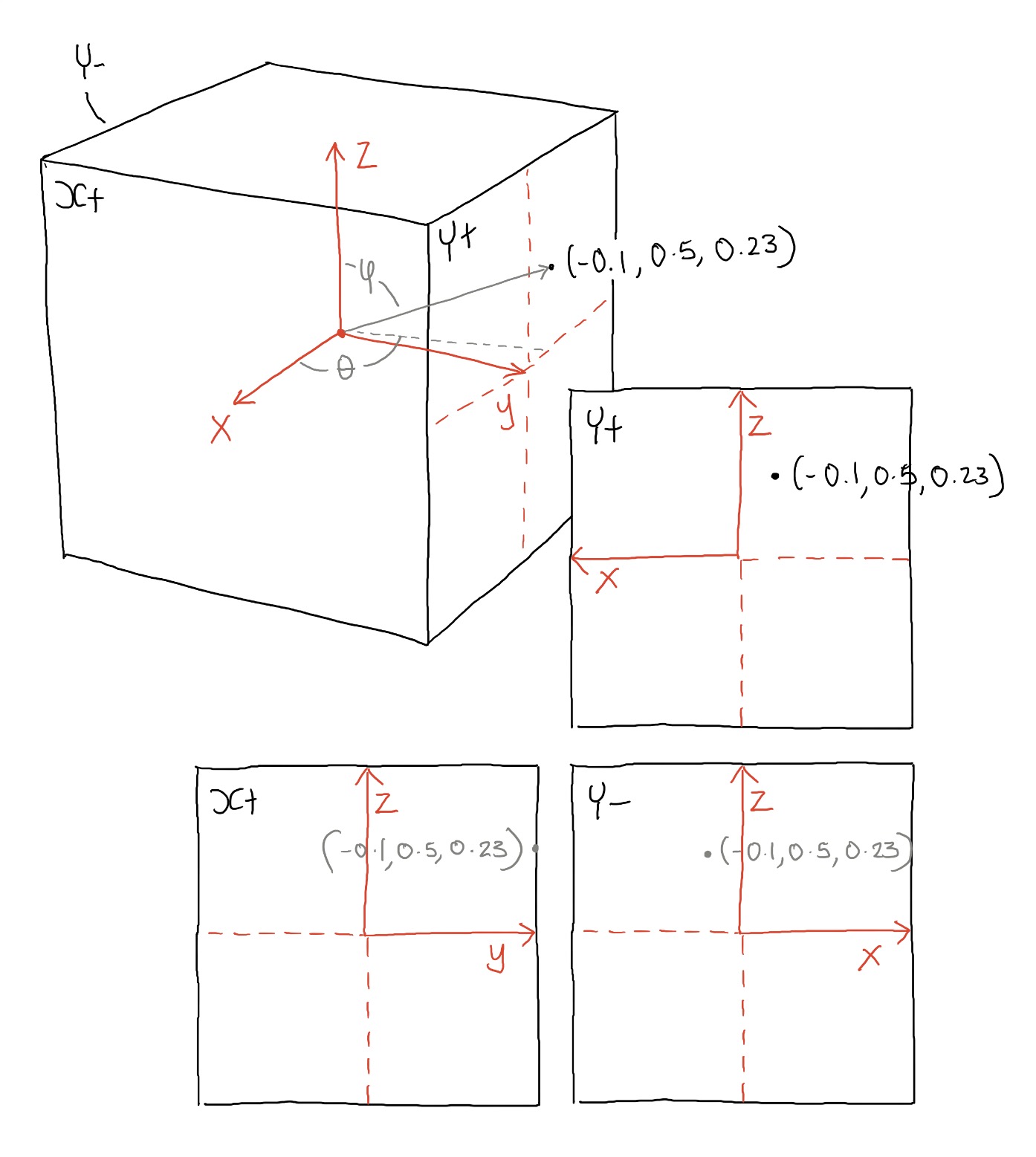
Depending on which face you're on, the axis orientation swaps around as you can see above. On the positive Y face, the X axis points to the right, in Y- it points to the left. We need to change this for each of the faces so that the bottom left corner is xy (0,0) and the top left is (1,1) - as you can see this will be slightly different for each face.

This is quite a simple process to convert between the two coordinates using the code below:

def unit3DToUnit2D(x,y,z,faceIndex):

    if(faceIndex=="X+"):
        x2D = y+0.5
        y2D = z+0.5
    elif(faceIndex=="Y+"):
        x2D = (x*-1)+0.5
        y2D = z+0.5
    elif(faceIndex=="X-"):
        x2D = (y*-1)+0.5
        y2D = z+0.5
    elif(faceIndex=="Y-"):
        x2D = x+0.5
        y2D = z+0.5
    elif(faceIndex=="Z+"):
        x2D = y+0.5
        y2D = (x*-1)+0.5
    else:
        x2D = y+0.5
        y2D = x+0.5

    y2D = 1-y2D

Notice that at the end I change the orientation of the Y axis - this is due to the fact I'm using python and the y axis is flipped so that (0,0) is the top left corner of the image.

So at this stage we know what face we're looking at, and what pixel within that face. There is now just one final step in the process and that is to work out where the faces are located within the input image. This is a very simple process, but varies according to what input images you have, and what layout they take. So your cube map may be set up as a cross, or a rectangular series of images such as demonstrated below:

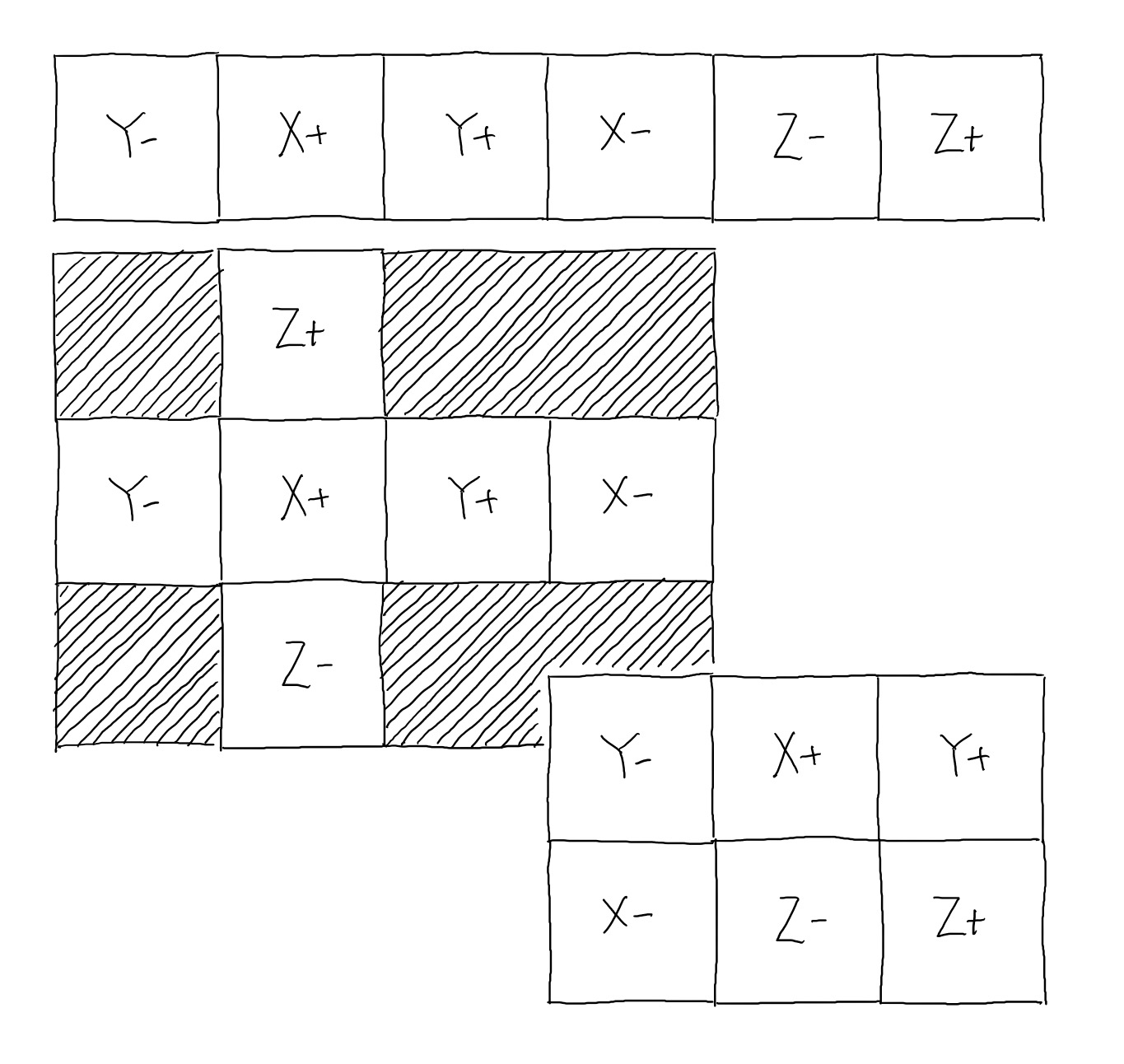
I use a simple function to shift the face coordinates to the correct location in the cube map:

def offset(x,y,face):

    if(face=="X+"):
        ox = 1
        oy = 0
    elif(face=="X-"):
        ox = 3
        oy = 0
    elif(face=="Y+"):
        ox = 2
        oy = 0
    elif(face=="Y-"):
        ox = 0
        oy = 0
    elif(face=="Z+"):
        ox = 5
        oy = 0
    elif(face=="Z-"):
        ox = 4
        oy = 0

    ox *= squareLength
    oy *= squareLength

    return {"x":x+ox,"y":y+oy}

That's all there is to it!

RESULTS

Images showing the input in the form of a strip, the output and what the result looks like running in my VR app:

CUBE MAP LAYOUT

As I mentioned above there are various cube map layouts you can use, some examples are shown in the image below; this list is in no way exhaustive! The format I'll be using is the one shown in red, however you can use any layout of your choice. Once you know the layout you're using all you need to do is cycle through each of the pixels in this output image. I'll be starting at the top left pixel, moving across the image and then down.

3D CARTESIAN COORDINATES

I'm cycling through all of the pixels in the output image. to begin with I need to know which face that pixel belongs to. This isnt a particulatly difficulat challenge - for example if the pixel is in the left third of the image and the top half - it is clearly the negative Y face. If it is in the right third and the bottom half it is in the poisitive Z face. the method you use will depend on the cube map layout you use.

Once you know which face you're in you also need to convert the coordinates of the output pixel into some local coordinates for the cube map face. So, for example in the image below if we had a pixel (8,10) in the output it would be located within the negative Z face, we could then adjust the coordinates local to this face only - so in this case it would become (2,2):

Once you have a local coordinate relative to the current face you're on you just need to normalise this. For spherical coordinates it makes sense if the cube and the sphere are centered on 0,0,0 - so that's what we will do. We will normalise the cube map coordinates so they are in the range of -0.5 to +0.5. Normalising isn't a completely straight forward process as we're working with a cube where on some faces the axis swap around, for example on the positive X face the Y axis points to the right, on the negative X face the Y axis points to the left, you can see this demonstated below.

In the example we used above we're working with the negative Z face with a local coordinate of (2,2). We normalise this to begin with, we divide each coordinate by the cube map square size. So in this case each square size was six, giving us (0.33, 0.33). This currently ranges from 0 to 1, we need to to range from -0.5 to 0.5 so we subtract 0.5, giving (-0.16, -0.16).

Finally we need to rearrange the axis if required, you can see in the negative Z face below the Y axis is the horizontal axis and the X is the vertical. We also know we're on the negative Z face so we know that Z is the minimum value it can be, -0.5. putting all of this together we have the 3D cartesian coordinate, xyz(-0.16, -0.16, -0.5).

SPHERICAL COORDINATES

Converting to spherical coordinates is a very easy process, we simply use the equations below:

R = sqrt(X*X + Y*Y + Z*Z)

θ = atan2(Y/X)
φ = acos(Z/R)

Where θ is given in 2π radians and
φ is given in π radians

We can try this with the example cartesian coordinates given in the previous section, xyz(-0.16, -0.16, -0.5).

R = sqrt(X*X + Y*Y + Z*Z) = 0.5488

θ = atan2(Y/X) = -2.3562
φ = acos(Z/R) = 2.7167

2D CARTESIAN COORDINATES

We are now ready for the final step, we just need to convert our spherical coordinates back into something which we can use to interrogate the input image. For this we just normalise the spherical coordinates so they range from 0 - 1. We know θ ranges from 0-2π, and we know that π ranges from 0-π so we just divide θ by 2π to give U, and divide φ by π to give V:

U = θ/2π = -0.375 or 0.625
V = φ/π = 0.865

We now just move 62.5% along the X axis of the equirectngular input and then 86.5% from the top to the bottom of the image, giving the point shown in green below:

We repeat this process for all of the pixels in the output cube map image giving us something like the image below: